The 803 is a general purpose electronic computer. It solves problems by obeying previously prepared programmes of simple instructions automatically and at high speed: the term "general purpose" is used to indicate that programmes can be written for a very large variety of applications. Once the programme required to solve one problem has been prepared, it can be used time and again for the solution of similar problems.
The writer of a programme, or programmer, requires a detailed understanding of the problem which is to be solved, together with the ability to express the solution as a sequence of elementary arithmetical steps.
This guide comprises an introduction to programming, with particular reference to the 803, and it is specifically intended for the reader with little or no programming knowledge.
An extensive collection of programmes is available for use with the 803, and full details are given in the publication "The Elliott 803 Library of Programmes". Reference is made to some of these in this guide, and it is shown that use can be made of them to reduce the work of solving new problems.

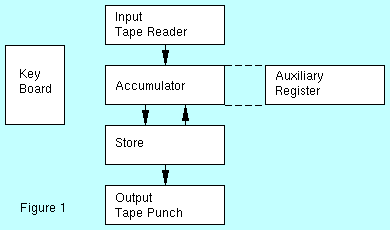
Figure 1 shows the parts of the computer with which the programmer is concerned. There exists also, of course, control and arithmetic units, which respectively cause and enable the computer to carry out it's programme. Detailed knowledge of these devices is not essential to a programmer.
The instructions to be obeyed and the data to be used in a calculation are placed in the store before the calculation commences, and remain there until actually required, when they pass from it to the control and arithmetic units at a suitably high speed. Without such an arrangement, the effective speed of the computer would be limited by the delays incurred in feeding each instruction and number in, and taking out each answer, including intermediate answers, by some manual or mechanical method.
The store of the 803 is divided into many different compartments termed locations; there may be 1024, 2048, 4096 or 8192 of these. Each location can hold one word, that is: one number or two instructions. The locations are numbered from 0 upwards, the number of each location being referred to as its address. The word stored in a location, whether it be a number or two instructions, is termed that location's content, e.g. the word store in the location whose address is 456 is "the content of location 456", which is written "C(456)".
In describing the actionof the computer, the letter N will frequently be used to to represent the address of a location: C(N) therefore indicates the "content of location N". In abridged notation, C(N) is written n.
Locations 0 to 3 are reserved for a special purpose, as will be explained later, but each of the remaining locations may be used for instructions or data, the allocation being at the discretion of the programmer.
In most arithmetical operations there are two operands. The usual manner in which 803 performs one step of a calculation is to take one number from its store, and perform some arithmetical operation with it and the number held in a device called the accumulator. This device, which is closely associated with the arithmetic unit, is capable of holding one word. It is denoted by A, and its content by C(A). In abridged notation, C(A) is written a.
In some operations an extension is required to the accumulator, and this extension is called the auxiliary register.
Punched cards may also be used as an input medium. A separate publication describes the method of use.
Each instruction is composed of two parts, denoted by F and N, of which:
To distinguish between the two uses of the number part of an instruction, we use N for the general case and for use (i), and N for use (ii).
| Name of | Function | Number | Effect |
|---|---|---|---|
| Instruction | F | N | |
| Replace | 30 | N | The existing C(A) is deleted, and |
| replaced by a copy of C(N). | |||
| Subtract | 05 | N | C(N) is subtracted from the exist- |
| ing C(A), which is deleted and | |||
| replaced by the difference. | |||
| Note: neither of the above actions affects C(N) itself. | |||
| Exchange | 10 | N | C(A) and C(N) are interchanged. |
| Double C(A) | 55 | N | C(A) is doubled N times |
| e.g. if N=5, the new C(A) will be | |||
| 32 times the old. | |||
Suppose that, at some stage in a calculation, the two numbers x and y are held in locations 5 and 6, and that it is required that (8x - y) be placed in location 7, for use later on. The instructions which the computer must obey to effect this are:
| F | N | Contents after obeying each instruction | ||||
|---|---|---|---|---|---|---|
| C(A) | C(5) | C(6) | C(7) | |||
| Initially... | ? | x | y | ? | ||
| 30 | 5 | x | x | y | ? | |
| 55 | 3 | 8x | x | y | ? | |
| 05 | 6 | (8x-y) | x | y | ? | |
| 10 | 7 | ? | x | y | (8x-y) | |
As mentioned in 1.2.1, instructions are held in the store, two instructions occupying one location. The instructions in the above example could be held, for instance, in locations 100 and 101. To express this we could write:
| Address | Instructions | |||
|---|---|---|---|---|
| F1 | N1 | F2 | N2 | |
| 100 | 30 | 5 | 55 | 3 |
| 101 | 05 | 6 | 10 | 7 |
Given the same starting point as that in Example 1, write the programme needed to cause the following to be placed in location 7.
| Name | F | N | Effect |
|---|---|---|---|
| Add | 04 | N | C(N) is added to the existing C(A), |
| which is deleted and replaced by the sum. |
Two unequal positive numbers, p and q, are held in locations 8 and 9, and these must be re-arranged, if neccesary, so that the lesser is in location 8, and the greater in location 9.
In order that the computer may determine whether a rearrangement is needed, it is designed to carry out what are termed conditional transfer functions, of which the following is typical:
| Name | F N | Effect | ||
| Transfer to first
instruction if C(A) is negative | 41 N | If the number in the accumulator is positive or zero,
the computer takes no action, and proceeds to the next instruction in normal sequence. | ||
|
But if the number in the accumulator is negative,
the computer breaks normal sequence, proceeds to obey the first instruction in location N, and then continues to obey instructions in sequence from that new point. |
Form the difference (p-q). If this is positive, a re-arrangement is necessary, so carry it out. But if (p-q) is negative, no rearrangement is required, so the rearrangement must be omitted.
The program is:
| Address | Instructions | |||||
| F1 | N1 | F2 | N2 | |||
| 150 | 30 | 8 | 05 | 9 | Form (p-q) in accumulator. | |
| 151 | 41 | 153 | 30 | 8 | If negative, omit these steps | |
| 152 | 10 | 9 | 10 | 8 | if positive, interchange 8 and 9 | |
| 153 | Next part of programme. | |||||
In the case instanced above, the computer is required to determine whether to "do something" or "not to do something". Where the problem requires a discrimination between "doing one thing" and "doing another", an unconditional transfer function may be useful as a complement to the conditional transfer. Such a function is:
| Name | F N | Effect | |
| transfer unconditionally to first instruction |
40 N | The computer breaks normal sequence, proceeds to obey the first instruction in location N, and then continues to obey instructions in sequence from that new point. |
Two different positive numbers are held in locations 24 and 25, and it is required to make both equal to the greater.
The scheme is:
Compare C(24) and C(25). If C(24) is the greater, place a copy in location 25 and proceed to the next part of the programme. If C(25) is greater, place a copy in location 24, and proceed to the next part of the programme.
The unconditional transfer is used to effect the underlined step, as the programme shows:
| Address | Instructions | |||||
| F1 | N1 | F2 | N2 | |||
| 250 | 30 | 24 | 05 | 25 | ||
| 251 | 41 | 253 | 30 | 24 | If C(24) is greater, place a copy in location 25, and skip the next two instructions |
|
| 252 | 10 | 25 | 40 | 254 | ||
| 253 | 30 | 25 | 10 | 24 | If C(25) is greater, place a copy in location 24. | |
| 254 | Next part of programme. | |||||
It is not always convenient to have two parts of a programme in adjacent sections of the store. For instance, in Example 3 the next part of the programme might be in locations 500, 501.....
In such cases, an unconditional transfer instruction would be inserted at the end of one section to cause the computer to transfer to the next.
| Contents | Next Chapter |